帺揮幵偲曕峴幰偺徴撍帠屘偱丄曕峴幰偑庴偗傞徴寕
乮仸偛幙栤偔偩偝偭偨曽偵嫋壜傪偄偨偩偄偨偺偱丄幙栤偲夞摎傪揮嵹偟傑偡丅偍柤慜傗奺庬偺悢抣偼幚嵺偺傕偺偲偼堎側傝傑偡丅乯
仧幙栤
丂揷拞乲壖柤乴偲偄偄傑偡丅
丂曕峴幰偵丄帺揮幵偑徴撍偟偨帠屘偱偡丅曕峴幰偼棫偭偰偄傑偟偨乮掆巭偟偰偄傑偟偨乯丅曕峴幰偵丄憱峴偟偰偒偨帺揮幵偑徴撍偟丄傇偮偐傜傟偨曕峴幰偼丄幬傔屻曽偺揹怣拰偵徴撍偟偰巭傑傝傑偟偨丅曕峴幰偑棫偭偰偄偨埵抲偲丄揹怣拰偺娫偼丄栺侾乵倣乶偱偡丅
丂帺揮幵偺幵廳偼俀俁乵倠倗乶丄忔堳偺懱廳偼係俆乵倠倗乶偱偟偨丅帺揮幵偺憱峴懍搙偼丄俀侽乵倠倣乛倛乶掱搙偩偭偨偼偢偱偡丅徴撍屻丄帺揮幵偼傾僗僼傽儖僩楬柺偺忋偵幬傔曽岦偵搢傟傑偟偨丅帺揮幵偑巭傑偭偨埵抲偼丄徴撍埵抲偐傜係乵倣乶偱丄憱偭偰偒偨曽岦偵懳偟偰塃幬傔俀侽搙偺曽岦偱偡丅
丂徴撍帪娫偑丄侽丏侽俆乵昩乶偩偭偨偲偡傞偲丄帠屘偱曕峴幰偑庴偗偨徴寕壸廳偼偳偺偔傜偄偺傕偺偱偟傚偆偐丅
仧夞摎
丂暔棟妛偱偼丄尰徾傪暘愅偡傞嵺偵偼丄尰徾偺摿挜傪偱偒傞偩偗巆偟偮偮丄寁嶼偑壜擻側傛偆偵乽儌僨儖壔乿傪峴偄傑偡丅丂儌僨儖壔偼丄嵄嵶側塭嬁傪柍帇偟偰戝榞傪懆偊傞偨傔偵昁梫側嶌嬈偱偡丅嵶偐側忬嫷傪憐掕偡傟偽丄嵺尷側偔暋嶨側偙偲傪峫偊傞偙偲偼偱偒傑偡偑丄暘愅弌棃傞掱搙偵娙扨壔傪峴偆偙偲偱丄杮幙揑側晹暘傪拪弌偟偰峫偊傑偡丅乮椺偊偽丄崱夞偺偛幙栤偺審偵偍偄偰丄曕峴幰偑拝偰偄偨暈偑僔儍僣偱偁傞応崌偲僕儍儞僷乕偱偁傞応崌偵偼丄庴偗傞徴寕偼傢偢偐偵堘偆偼偢偱偡偑丄偦偺傛偆側嵎偼峫椂偟側偄偲偄偆偙偲偱偡丅乯
丂
丂揷拞條傛傝偄偨偩偄偨暥柺偐傜偱偡偲丄寁嶼偺偨傔偵偼偄偔偮偐壖掕傪偡傞昁梫偑偁傝傑偡丅棫偭偰偄偨曽偼墶搢偟偵側傞傛偆偵搢傟偨偺偐怟栞傪偮偔傛偆側忬懺偵側偭偨偺偐丄帺揮幵偑揮搢偟偨埵抲傗揮搢屻偺帺揮幵偲忔堳偼偳偺傛偆偵揮偑偭偨偺偐側偳偑晄柧偱偡偟丄恖懱偺暔棟揑側惈幙偼岦偒傗椡偺偄傟嬶崌側偳偵傛偭偰曄壔偟傑偡丅
偙偺傛偆側棟桼偐傜丄偲傝偁偊偢偼扨弮側暯柺忋偺徴撍偱偁偭偨偲偟偰夝愅傪峴偄傑偡丅乮徻嵶側忦審偑傢偐傟偽嵞搙儌僨儖壔偟偰寁嶼偼壜擻偱偡丅乯
徴撍偺條巕傪丄壓恾偺傛偆偵儌僨儖壔偟傑偟偨丅
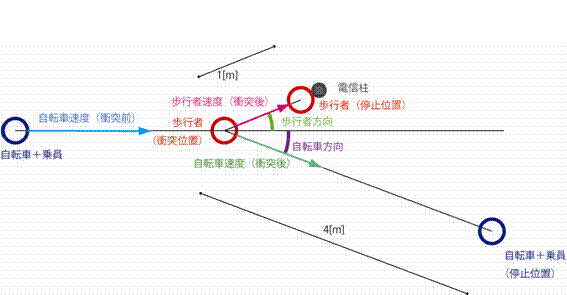
帺揮幵偲忔堳偑堦懱偲側偭偰恾偺嵍偐傜塃曽岦偵憱偭偰偒偰丄棫偭偰偄傞乮巭傑偭偰偄傞乯曕峴幰偵徴撍偟偨偲偟傑偡丅帺揮幵偼憱偭偰偒偨曽岦偐傜傒偰乽帺揮幵曽岦乿暘偩偗堩傟偰揮搢偟丄徴撍埵抲偐傜係乵倣乶愭偱掆巭偟傑偟偨丅曕峴幰偼帺揮幵偺憱偭偰偒偨曽岦偐傜傒偰乽曕峴幰妏搙乿暘偩偗幬傔偵撍偒旘偽偝傟傑偟偨偑丄侾乵倣乶棧傟偨揹怣拰偵徴撍偟偰掆巭偟傑偟偨丅
偛幙栤偱偼丄乽曕峴幰偑庴偗偨亀徴寕壸廳亁乿傪媮傔偨偄偲偺偙偲偱偟偨偑丄徴寕壸廳偼丄婎杮揑偵偼抏惈懱乮椡傪榗傒偱庴偗巭傔丄偦偺椡偑偐偐傜側偔側傞偲尦偺宍偵栠傞傛偆側暔懱丅揝斅傗價乕嬍側偳傪偍峫偊偔偩偝偄乯偳偆偟偺徴撍偺偲偒偵惗偠傞徴寕傪昞偡検側偺偱丄帺揮幵偲曕峴幰偺徴撍傪昞偡偨傔偵偼偁傑傝揔偟偰偄傑偣傫丅偦偺偨傔丄埲壓偱偼丄恖懱偑徴撍偵傛偭偰乮掆巭偟偨忬懺偐傜乯壛懍偝傟偰揹怣拰偺曽岦偵摦偄偨偙偲偐傜丄偦偺摦偒傪惗偠傞偨傔偵摥偄偨椡傪媮傔偰丄徴寕偺嫮偝偲偟傑偡丅
傑偨丄恖懱偲帺揮幵乮亄忔堳乯偺徴撍偵偮偄偰偼丄姰慡旕抏惈徴撍乮斀敪學悢侽丗擲搚傗晍抍偳偆偟偺徴撍偺傛偆側忬懺乯偱偁傞偲偟丄徴撍屻傕帺揮幵偲忔堳偼堦懱偲側偭偨傑傑堏摦偟偨偲峫偊傑偡丅
悢幃傪棫偰傞偨傔偵丄偍偺偍偺偺抣傪婰崋偱帵偟傑偡丅
M = 帺揮幵偺廳偝亄忔堳偺廳偝丂亖丂23[kg] + 45[kg] = 68[kg]
m = 曕峴幰偺廳偝丂亂揷拞條偼擔杮恖偺暯嬒懱廳 55[kg]偲偟傑偡亃
V0 = 帺揮幵偺憱峴懍偝乮徴撍捈慜偺懍偝乯 = 20[km/h]
V1 = 帺揮幵乵亄忔堳乶偺徴撍屻偺懍偝
V2 = 曕峴幰偺徴撍屻偺懍偝
兤1 = 帺揮幵曽岦乮徴撍屻偵傕偲偺恑峴曽岦偐傜堩傟偨妏搙乯 = 20[搙]
兤2 = 曕峴幰曽岦乮徴撍屻偵摦偄偨曽岦偲帺揮幵偑恑傫偱偒偨曽岦偺側偡妏搙乯
t2 = 徴撍帪娫乮帺揮幵偲曕峴幰偑愙怗偟偰偄偨帪娫乯 = 0.05[昩]
悈暯曽岦傪倶嵗昗丄悅捈曽岦傪倷嵗昗偲偟傑偡
乮悢幃偺揥奐偼揔媂愢柧傪擖傟傑偡偑丄幃傪拃堦捛偄偐偗傞昁梫偼偁傝傑偣傫丅乯
亂寁嶼亃
丒姰慡旕抏惈徴撍偱偁傞偙偲偐傜丄徴撍捈屻偵偼丄帺揮幵偺倶幉曽岦懍偝偲曕峴幰偺倶幉曽岦懍偝偼摍偟偄偺偱
亪 ![]() 乧丂嘆
乧丂嘆
塣摦検曐懚懃偐傜
倶幉曽岦丗![]() 丂乧丂嘇
丂乧丂嘇
倷幉曽岦丗![]() 乧丂嘊
乧丂嘊
偙偺拞偱枹抦偺抣偼丄V1, V2, 兤2偺嶰偮側偺偱丄嘆乣嘊幃傪楢棫曽掱幃偲偟偰夝偗偽丄偦傟偧傟偺抣偑傕偲傑傝傑偡丅乮仸尩枾偵悢妛揑偵尵偆偲丄嶰妏娭悢傪娷傫偱偄傞偺偱俁幃偐傜媮傑傞偲偼尷傜側偄偺偱偡偑丄偙偺応崌偵偼夝偔偙偲偑偱偒傑偡丅乯
嘆傛傝
![]() 乧嘆乫
乧嘆乫
嘇偵戙擖偡傞偲
![]()
堦斒揑偵
![]()
偱偁傞偙偲偐傜
![]()
嘊偵戙擖偟偰丄V1偵偮偄偰夝偔偲
![]() 丂乧嘊乫
丂乧嘊乫
偲側傝傑偡丅偙傟傛傝丄V1乮帺揮幵乵亄忔堳乶偺徴撍屻偺懍偝乯偑媮傑傝傑偡丅
![]()
佮11.77[km/h]=3.27[m/s]
嘆乫幃傪嘊乫偵戙擖偡傞偲
![]()
椉曈傪帺忔偟偰惍棟偟丄V2偵偮偄偰夝偔偲
![]() 丂乧丂嘋
丂乧丂嘋
偲側傝傑偡丅偙傟傛傝V2乮曕峴幰偺徴撍屻偺懍偝乯偑媮傑傝傑偡丅
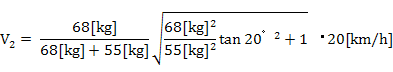
佮12.12[km/h] = 3.37[m/s]
嘊乫偲嘋傪嘆乫偵戙擖偟偰惍棟偡傞偲

亪
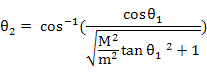
偙偙偐傜兤2偑媮傑傝傑偡丅
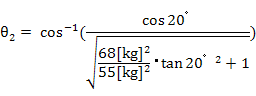
佮31.03並
帺揮幵乵亄忔堳乶偲曕峴幰偺娫偵椡偑壛傢偭偰偄偨偺偼丄徴撍帪娫t2偺娫偩偗偱偡偐傜丄曕峴幰偼t2偺帪娫偱懍偝侽偐傜V2傑偱壛懍偝傟偨偙偲偵側傝傑偡丅徴撍帪娫偺娫偵曕峴幰偵偐偐偭偨壛懍搙a2偑堦掕偩偭偨偲偡傞偲丄偦偺抣偼
![]()
佮67.4[m/s2]
偲側傝傑偡丅
椡偼廳偝偲壛懍搙偺愊偱偁傞偙偲偐傜丄徴撍帪娫偺娫偵曕峴幰偵偐偐偭偨椡F2偼
![]()
佮3704.8[N] = 378.04[kg廳]
偲媮傑傝傑偡丅
亂寢榑亃
寁嶼寢壥傪傑偲傔傞偲丄
帺揮幵乵亄忔堳乶偺徴撍屻偺懍偝丂丗丂栺11.77[km/h]丂乮3.27[m/s]乯
曕峴幰偺徴撍屻偺懍偝丂丗丂栺12.12[km/h] 丂乮3.37[m/s]乯
曕峴幰曽岦丂丗丂栺31搙
曕峴幰偵偐偐偭偨椡丂丗丂栺3700[N] 乮378[kg廳]乯
偱偁偭偨偙偲偵側傝傑偡丅
偮傑傝丄曕峴幰偵偲偭偰偼丄0.05昩娫偺娫偱偼偁傝傑偡偑丄偍憡杘偝傫俀恖偵摨帪偵摜傑傟偨偺偲摨摍偺徴寕傪庴偗偨偙偲偵側傝傑偡丅
側偍丄偙偙偱偺寁嶼偱偼丄曕峴幰偑揹怣拰偵徴撍偟偨偲偒偺徴寕偼峫椂偟偰偄傑偣傫丅偨偨傜傪摜傓傛偆偵棫偭偨傑傑偱揹怣拰傑偱堏摦偟偨偐丄搢傟崬傒側偑傜恎懱偺堦晹偑揹怣拰偵徴撍偟偨偐側偳偺宍懺偵傛偭偰丄揹怣拰偵徴撍偟偨偲偒偺徴寕偼曄壔偟傑偡丅
揷拞條偐傜偺偛幙栤偺暥柺偐傜媮傔傜傟傞偺偼偙偺掱搙偺斖埻偱偡偑丄揹怣拰偵扏偒偮偗傜傟傞傛偆偵徴撍偟偨偺偱偁傟偽丄揹怣拰偵徴撍偟偨偲偒偺徴寕傕憡摉戝偒側傕偺偱偡偟丄帺揮幵偺憱峴懍搙偑傕偭偲崅偐偭偨偙偲傪帵偣傞壜擻惈傕偁傝傑偡丅
嵞寁嶼傗丄偛擖傝梡偱偟偨傜娪掕彂偺嶌惉傕彸傝傑偡丅
埲忋丄傛傠偟偔偍婅偄偄偨偟傑偡丅
岎捠帠屘娪掕儔僾僞乕
拞搰攓