1.インバースカメラメソッド
道路を俯瞰(斜めに見下ろした)した写真にうつっている「平行四辺形を基準」にして、道路を真上から見た写真を再現する方法です。
再現した写真は、土木測量によって作られた図面と同じように扱えるため、 CADソフト(設計・製図を精密に行う専用のコンピュータプログラム)を利用することで、
再現写真上で長さを測定したり、痕跡の形を確認することができます。
インバースカメラメソッドは、基準となる平行四辺形の寸法がわかれば適用できます。例えば、事故発生後に道路が改修され、我々が調査に行っても事故の痕跡が確認できないような状況だったとします。しかし、実況見分調書の写真などにインバースカメラメソッドを適用して、事故痕跡の再現が可能なこともあります。実際にインバースカメラメソッドを適用できるか否かは撮影されている写真によります。デジカメデータを電子メールに添付するか、焼き増しした写真を送付いただければ、回答いたしますので、お気軽にお問い合わせください。
  
適用例
直進車の前に歩行者が飛び出したために事故になったとされた案件
◇現場写真
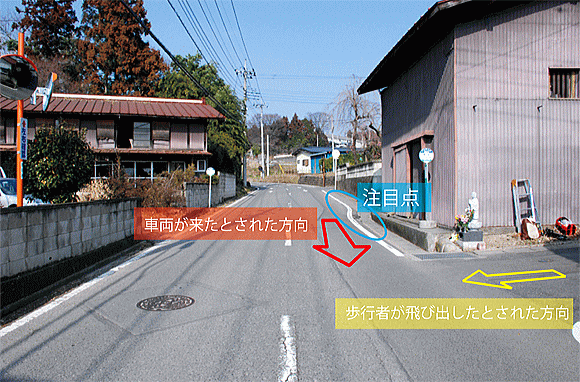
自動車の運転手は、写真の奥から手前方向に車線を守って直進してきたところ、写真左側のT字路から歩行者が飛び出してきたため避けられなかったと言いました。歩行者は、衝突後まもなく亡くなったため、証言はありません。
我々は、自動車が衝突する直前に通過した道路位置の側線に注目しました。(上の写真で「注目点」として囲んだ部分です。)明らかに道路の側線が曲がっています。
◇道路台帳図
そこで、自治体が持っている道路台帳図(道路の維持・管理のために自治体が持っている公式な測量地図)を入手して、事故地点付近の道路の寸法を知ろうとしました。
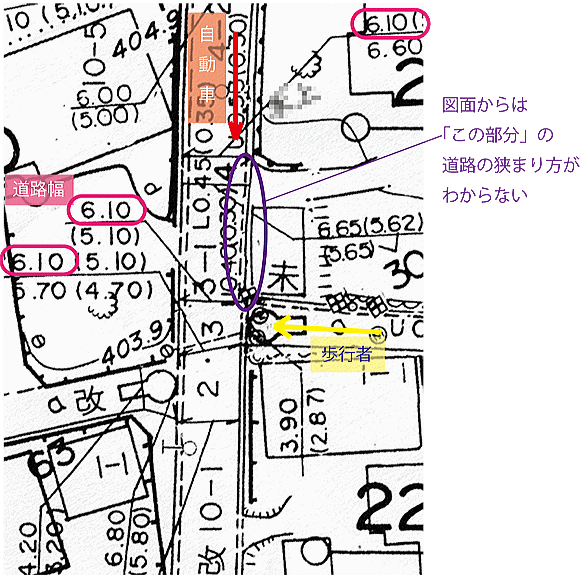
しかし、道路台帳図では、事故現場付近の道路幅が、間隔をおいて測定されているだけで、曲がっている側線の様子は読み取れませんでした。
◇インバースカメラメソッド
そこで我々は、インバースカメラメソッドを利用することにしました。インバースカメラメソッドは、前述のように、写真に写っている平行四辺形を基準として、真上から撮影した写真を構成する手法です。
この案件では、現場写真の左下に、正方形のマンホールの補修痕跡が写っていたので、これを利用しました。
現場写真にインバースカメラメソッドを適用して得られた画像を以下に示します。
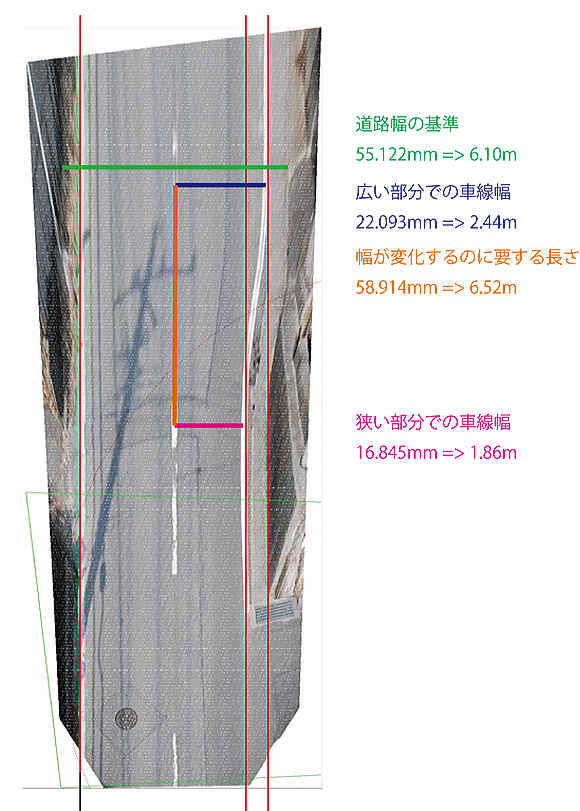
側線に沿った縦の3本の直線の直線は、一番左の直線(左側の側線の道路外側の境目)と平行に、道路右側の狭い部分と広い部分の位置に合わせて描いたものです。道路の直線部分の直線性や平行性がよく確認できます。
このように、インバースカメラメソッドを利用して作成した画像では、どのようなポイント間の長さの比であっても、現場でのポイント間の長さの比と等しくなります。(もとの写真の大きさや解像度が関係するので、あくまで長さの比が等しくなります。)
画像をCADソフトウェアに取り込んで長さを測ると、道路の幅は55.122[mm]、自動車が走行してきた車線の広い部分の幅は22.093[mm]で狭い部分の幅は16.845[mm]でした。また、車線が広い部分から狭い部分に変化するまでの進行方向の長さは58.914[mm]でした。
道路台帳図からわかるように、道路の広い部分の幅は6.1[m]です。このことから、
- 広い部分での車線幅 2.44[m]
- 狭い部分での車線幅 1.86[m]
- 車線が広い部分から狭い部分に変わるまでの長さ 6.52[m]
であることがわかります。
つまり、自動車から見ると、6.52[m](車体の長さの約1.5倍)の距離を進む間に、車線幅が0.58[m](=2.44−1.86。車体の幅の約1/3)も急に狭まることになります。
この案件では、他の証拠から、歩行者との衝突の際に自動車が道路外側向き(歩行者が飛び出してきたとされる道路に曲がる向き)で走っていたことがわかっていました。前述のように、インバースカメラメソッドを利用した解析では、自動車からは、自車線が側線側から急激に狭まったことがわかりました。このような状況では、自動車は道路中央方向に曲がることはありえますが、自車線を守って走行してきて道路外側向きに曲がるというのは極めて不自然です。
我々の鑑定では、自動車はそもそも自車線を守らずはみ出し走行をしてきたところ、何らかの原因(対向車が来たなど)で自車線に戻ろうとしたが、不注意で歩行者に気付かず、衝突したと結論しました。当該事故では、自動車の運転手は不起訴でしたが、検察審査会によって不起訴不当の議決がなされました。
↑ページの先頭へ
|

